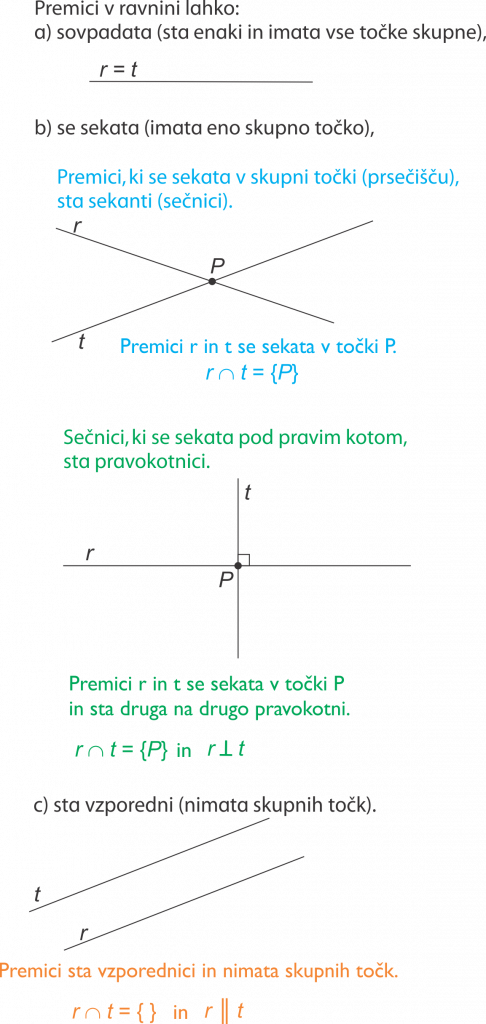
OSNOVNI GEOMETRIJSKI POJMI

Odnosi med geometrijskimi elementi v ravnini

1. Razlaga učne snovi.

UVODNA MOTIVACIJA, RAZMISLEK:

Mikado je stara japonska igra, ki se igra z 41. barvnimi lesenimi paličicami. Vrednost določajo barve (od izdelovalca igre je odvisna barvna kombinacija paličic in njihovo število). V igri lahko sodeluje več igralcev. Eden izmed njih paličice vzame v desno roko, na sredini jih stisne. Nato jih postavi pokonci nad mizo, na katero jih hitro spusti. Paličice padejo na mizo v krogu. Pravila igre: KLIK

Ali se dve paličici vedno sekata, ko jih na začetku spustimo na mizo?

Odgovor

Paličicela lahko padejo po mizi tudi tako, da se ne sekajo ali pa da so vzporedne. Torej ni nujno, da se vedno sekajo.

2. Zapiši in nariši v zvezek

V SDZ na strani 47 in 48 si preberi:
1. Kako s simboli označimo lego točke na premici.
2. V kakšnem medsebojnem odnosu sta lahko premici, ki ležita v ravnini.

3. Povezave za dodatno delo

Na spletni strani iUčbeniki si oglej poglavje o pravokotnicah.
Na spletni strani iUčbeniki si oglej poglavje o vzporednicah.

4. Domača naloga

Za doma naredi naloge iz SDZ str. 49, 50/1, 2, 3, 4, 5, 6, 7.

Classcraft izziv za 300 XP

Nariši po navodilu celotno sliko.

Premici p in r se sekata, a ne pravokotno, v točki V.
Na premici p leži točka M in na premici r točka N.
Skozi točko M nariši pravokotnico a na premico r.
Skozi točko N nariši pravokotnico b na premico r.
Presečišče premic a in r označi s točko O in presečišče
premic b in p s točko P.
a) Zapiši odnose med narisanimi premicami z besedami.
b) Na narisani sliki preštej število presečišč, daljic in premic.

Rešeno nalogo pošlji Gamemasterju.