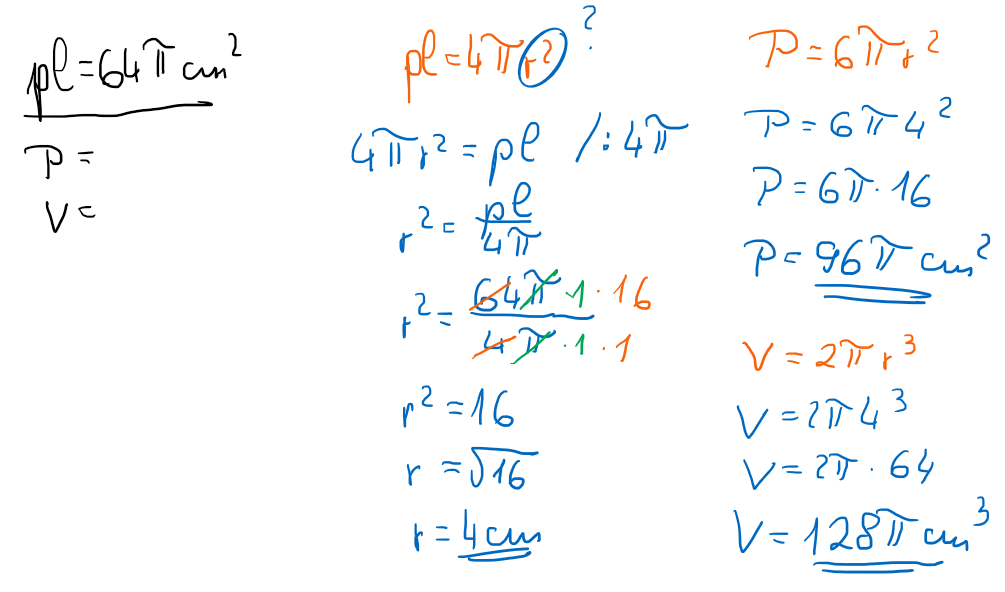VALJ

Enakostranični valj

1. UVODNA MOTIVACIJA, RAZMISLEK:

Sekanje drv je kar težaško delo. Ročno to počnejo s sekiro za večje hlode pa si pomagajo z raznimi rezalno-cepilnimi stroji in žagami.
Na zgornji levi sliki vidiš, kako si je mojster na Kovku pripravil drva, na desni pa primer na pol presekanega hloda, ki ima obliko valja.

 

  • Kateri geometrijski lik nastane, ko hlod presekamo točno po sredini?
  • Kako dobimo osni presek valja?
  • Katere so vse 4 možnosti (kateri liki), ki jih lahko dobimo za osni presek pri pokončnih in poševnih valjih?

Prerez

Če hlod presekamo ali prežagamo natanko po sredini, torej čez središči obeh osnovnih ploskev, ima prerez obliko pravokotnika.

Osni presek valja

Osni presek valja  dobimo tako, da valj sekamo z ravnino, ki gre skozi središči obeh osnovnih ploskev. Namišljeno premico, ki gre skozi središči osnovnih ploskev imenujemo os.

Možnosti

Osni presek pokončnega valja je lahko pravokotnik ali pa kvadrat. Osni presek poševnega valja je lahko paralelogram ali pa romb. Slednjih ne bomo obravnavali, prav gotovo jih pa pri sekanju polen lahko opazimo.

2. RAZLAGA IN ZAPIS V ZVEZEK

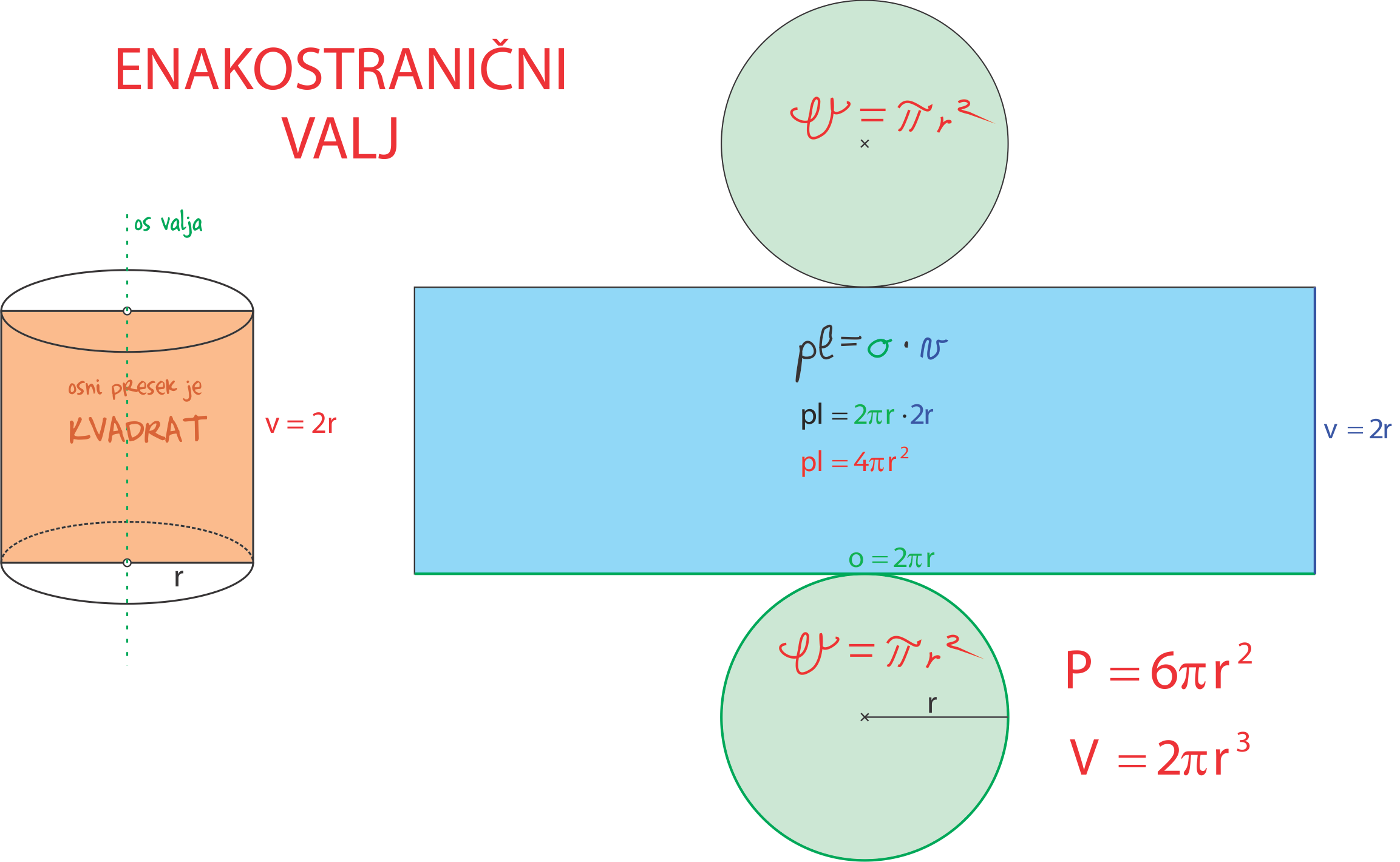
Zapiši naslov ENAKOSTRANIČNI VALJ in preriši spodnjo razlago v zvezek.

Površino enakostraničnega valja lahko izračunamo s formulo P = 6πr2,

prostornino pa po formuli V = 2πr3, kjer r pomeni polmer osnovne ploskve valja (kroga).

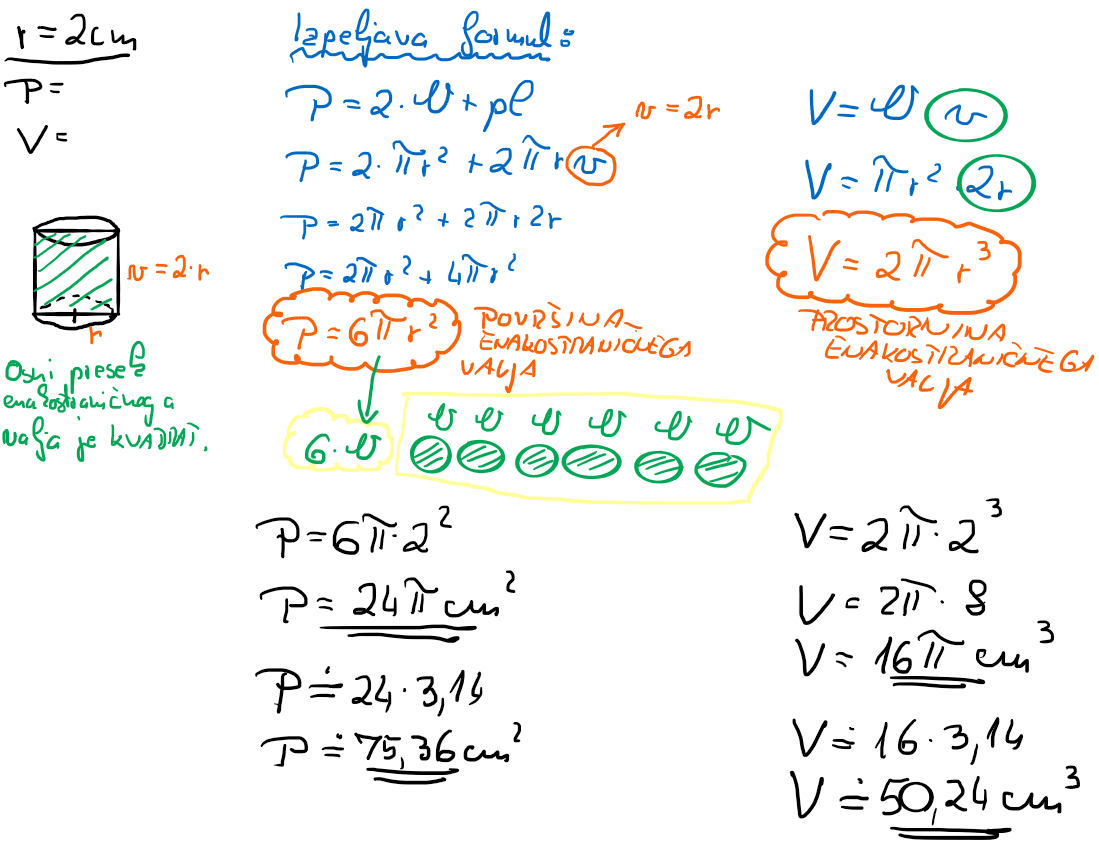
1. NALOGA: Izpelji formulo za izračun površine in prostornine enakostraničnega valja s polmerom 2 cm. Nato še izračunaj P in V valja.

2. NALOGA: Izračunaj površino in prostornino enakostraničnega valja s plaščem 64π cm2.

3. POVEZAVE ZA DODATNO DELO

  • Na spletni strani iUčbeniki  za izziv poskusi rešiti 25. in 29.  nalogo.

4. DOMAČA NALOGA

Za doma naredi naloge iz SDZ str. 73, 74, 75/
A težavnost: 1, 2, 3, 4
B težavnost: 1,4, 5, 6, 9

Naloga za izziv: Ali lahko Franc dvigne bukov hlod dolžine 1 meter, če veš, da je premer bukve 60 cm? Odgovor utemelji. Potrebne podatke, ki jih potrebuješ za odgovor poišči sam. 💪

  Slikaj, shrani kot .jpg
9r_DN#_Priimek_Ime.jpg
Npr.:
 NALOŽI!
(Visited 2.194 times, 1 visits today)